For the past few months since the election, I've been looking for a math project to work on until election prediction becomes a useful thing again. I've decided to take a shot at looking at climate data.
Does this make me a climate skeptic? Why don't I just accept the consensus of professionals?
Politically, I have more in common with the people who accept climate change than I do with those who doubt it or flat-out deny it. What I really want to do is make a set of rules I want both sides to follow. My system is still evolving, but I think I have it defined well enough to start explaining my methods and publishing my results.
To begin with, I'd like to thank the folks at Berkeley Earth Surface Temperature for creating the most complete database of temperature readings available to the public. Richard Muller founded the project with money supplied by the Koch Brothers, who have funded a lot of projects whose goal is to downplay climate change or deny it outright. Muller is a physicist at Cal and was considered a skeptic when he took their money. In point of fact, his skepticism was based on the fact that he is a physicist and the people doing climate science aren't. Physicists think they understand math better than people in other fields do, and they often are right.
When Muller finally published, he was no long skeptical about the numbers. Many people in the denialist community promised they would abide by whatever Muller found, but few have changed their minds.
Okay, why am I making this my new hobby?
I saw Muller speak last year and what interested me most was the database. I wanted to see if I could come up with a simple way to look at the patterns of change over time in regions. Everyone agrees that not all parts of the globe are changing at the same rate. My not very modest goal is to get rid of cherry picking in every case possible. The examples of cherry picking on the denialist side are legion, but both climate scientists and the press who accept global warming are also guilty of presenting the data in the best possible light, sometimes arriving at completely unsupportable conclusions. I want to make a set of rules for what defines a reasonable time period, most especially years that can start and end such periods, and a reasonable way to look at trends.
My software lets me look at any region that can be defined by a high and low longitude and a high and low latitude. (This means circles or arcs of circles if the North or South Pole are included, and rectangles on Mercator projections, which look more like slices of rings when mapped in any area preserving projection system.)
I will be explaining the system over the next several posts and will present my findings once I have defined the rules.
I will end each post on this topic with my motto.
Death to cherry picking and woe to cherry pickers.
Thursday, January 31, 2013
Wednesday, January 30, 2013
Rational points on the unit circle and the Pythagorean triples.
Trigonometry translated from it Greek roots means "the measure of triangles", most notably right triangles. The most important aspect of right triangles is the Pythagorean Theorem, usually stated as a² + b² = c².
The unit circle on the xy plane is given by the formula x² + y² = 1. There are infinitely many points on the circle and if you pick one truly at random, it will very likely be irrational, which means neither the x or the y be written as p/q, where p and q are whole numbers. The only way it is possible for a point on the unit circle to be rational is to have two fractions of the form a/c and b/c where a² + b² = c². For example,
(3/5)² + (4/5)² = (5/5)² = 1.
In Excel, I generated 26 rational points on the unit circle, the largest denominator being 1,105. As you can see, there are a lot of gaps, but you can make out the general shape of a quarter circle.
Here's what it looks like with 662 rational points plotted. You can still see some gaps, notably near the horizontal lines at 0.8 and 0.6. If all the rational points were plotted, and there are infinitely many, you would not be able to see any gaps with the naked eye or at any magnification. In math, we say that the set of rational points is dense on the unit circle.
But here's one of the goofy things about infinity. There are also infinitely many points on the unit circle where both values are irrational AND infinitely many points where x is rational and y irrational AND infinitely many points where x is irrational and y rational. Let me write those sets out.
Set #1: { the set of points on the unit circle where both x and y are irrational}
Set #2: { the set of points on the unit circle where both x and y are rational}
Set #3: { the set of points on the unit circle where x is rational and y irrational}
Set #4: { the set of points on the unit circle where x is irrational and y rational}
All four of those sets are dense on the circle, meaning that in any segment of the circle no matter how small, there will be elements from all four of the sets.
Here's something even weirder about infinity. Sets #2, #3 and #4 are all the same size of infinity, but Set #1 is a bigger size of infinity, bigger than the other three combined.
Tomorrow, we move from goofy facts about infinity to more practical math aimed at answering the question "Is climate change or global warming real?"
Tuesday, January 29, 2013
Using the generating function for relatively prime Pythagorean triples.
Yesterday's post ended with the statement of the generating function for Pythagorean triples. Take any two distinct whole numbers j and k and let j be the larger. Here are the formulas for a, b and c.
a = j² - k²
b = 2jk
c = j² + k²
Example #1: j = 2, k = 1
a = 4-1 = 3
b = 2 × 2 × 1 = 4
c = 4+1 = 5
Example #2: j = 3, k = 1
a = 9-1 = 8
b = 2 × 3 × 1 = 6
c = 9+1 = 10
Example #3: j = 3, k =2
a = 9-4 = 5
b = 2 × 3 × 2 =12
c = 9+4 = 13
Not surprisingly, using the three smallest pairs around (2, 1) (3, 1) and (3, 2), we get the three smallest Pythagorean triples. But notice that (3, 1) generates 8-6-10 which is not a relatively prime triple, since all the numbers are even. Looking at this carefully, we see that if both j and k are odd, this will make a, b and c even.
a = odd² - odd² = even
b = 2×odd×odd = even
c = odd² + odd² = even
To generate a relatively prime Pythagorean triple, we need two things to be true about j and k.
1. j and k must be relatively prime.
2. j - k must be odd. (Another way to state this is one is odd and the other even.)
Tomorrow, a few more rules about the relatively prime Pythagorean triples.
a = j² - k²
b = 2jk
c = j² + k²
Example #1: j = 2, k = 1
a = 4-1 = 3
b = 2 × 2 × 1 = 4
c = 4+1 = 5
Example #2: j = 3, k = 1
a = 9-1 = 8
b = 2 × 3 × 1 = 6
c = 9+1 = 10
Example #3: j = 3, k =2
a = 9-4 = 5
b = 2 × 3 × 2 =12
c = 9+4 = 13
Not surprisingly, using the three smallest pairs around (2, 1) (3, 1) and (3, 2), we get the three smallest Pythagorean triples. But notice that (3, 1) generates 8-6-10 which is not a relatively prime triple, since all the numbers are even. Looking at this carefully, we see that if both j and k are odd, this will make a, b and c even.
a = odd² - odd² = even
b = 2×odd×odd = even
c = odd² + odd² = even
To generate a relatively prime Pythagorean triple, we need two things to be true about j and k.
1. j and k must be relatively prime.
2. j - k must be odd. (Another way to state this is one is odd and the other even.)
Tomorrow, a few more rules about the relatively prime Pythagorean triples.
Monday, January 28, 2013
Generating Pythagorean triples.
The Pythagorean Theorem is usually stated as a² + b² = c². If all three numbers are whole numbers, it is called a Pythagorean triple. Here are some examples with small numbers as the entries.
3² + 4² = 5²
12² + 5² = 13²
15² + 8² = 17²
24² + 7² = 25²
21² + 20² = 29²
35² + 12² = 37²
In these examples, no number bigger than 1 divides all three numbers in the set, so these are the relatively prime Pythagorean triples. It is true that 6² + 8² = 10² (36+64=100), but this is just taking the 3-4-5 triangle and multiply each number by two.
Here are a few rules about the relatively prime Pythagorean triples.
They are always of the form odd² + even² = odd². We can have even² + even² = even², like 6-8-10, but all the numbers are divisible by two, so they aren't relatively prime. It turns out that odd² + odd² will be even, of course, but it can never be the square of an even number. All the even squares are divisible by 4 and the sum of two odd perfect squares will always have remainder 2 when divided by 4.
There is a generating function. Take any two distinct whole numbers j and k and let j be the larger. Here are the formulas for a, b and c.
a = j² - k²
b = 2jk
c = j² + k²
Tomorrow, we will look at what choices for j and k will produce the relatively prime Pythagorean triples.
Sunday, January 27, 2013
The 3-4-5 triangle
The Pythagorean Theorem is often stated as
a² + b² = c²
means that the sum of the squares of the lengths of the two short sides (the ones that meet to create the right angle) is equal to the square of the length of the long side opposite the 90°, the side known as the hypotenuse.
If you pick two whole numbers at random to be the short sides, also known as the legs, the hypotenuse will be a square root of a whole number.
For example: If a = 1 and b = 3, 1² + 3² = 10, which means c² = 10. 10 is not a perfect square, so c is equal to the irrational number the square root of 10, which I will write as sqrt(10).
If we are looking at one digit numbers only, we have just one pair of legs that will add up to a perfect square. 3² + 4² = 9 + 16 = 25 = 5².
Three whole numbers that satisfy a² + b² = c² are called a Pythagorean triple. If we find such a triple, we can create infinitely more by multiplying all the sides by the same whole number. Here are some examples.
Multiply 3-4-5 by 2: 6² + 8² = 10²
Multiply 3-4-5 by 3: 9² + 12² = 15²
Multiply 3-4-5 by 4: 12² + 16² = 20²
...
All of these triangles are similar and when discussing Pythagorean triples, the ones that are relatively prime are a special case.
The Pythagorean Theorem is named for the ancient Greek mathematician Pythagoras (570-495 BCE), but as often happens in math, this does not mean he was the first person ever to notice the pattern. There is strong evidence that the ancient Egyptians who built the pyramids understood the 3-4-5 triangle at the very least, and they lived thousands of years before Pythagoras. In many archeological digs, among the building tools are three sticks of lengths with the ratio 3:4:5. It is assumed that the builders used these when constructing walls to make sure the walls and the floors met at 90° angles.
There are other relatively prime Pythagorean triples; in fact, there are infinitely many. The next two smallest ones are 5² + 12² = 13² and 8² + 15² = 17².
Tomorrow, we will discuss how to create all the Pythagorean triples, both those that are relatively prime and those that aren't.
Saturday, January 26, 2013
Two picture proofs of the Pythagorean Theorem.
Here are two squares that are the same size. In the left square, we will label the blue square a² and the red square b². The two white rectangles both have area ab. Together, they show the famous "middle term" representation of
(a + b)² = a² + 2ab + b²
The square on the right has four white right triangles that are the equivalent of the two white rectangles sliced diagonally, where the diagonal is the hypotenuse, which we usually label c. The yellow square with the gap in it has area c². Since the squares are the same size we get
c² + 4(½ab) = a² + 2ab + b² Next step: get rid of the parentheses
c² + 2ab = a² + 2ab + b² Next step: subtract 2ab from both sides
c² = a² + b² and we are done.
Second proof just using the yellow square and the gap inside.
The gap in the middle of the yellow square is (a - b)² = a² - 2ab + b². The four yellow triangles are 2ab, exactly the same as the four white triangles. That means this picture tells us
c² = a² - 2ab + b² + 2ab
So we combine like terms to get
c² = a² + b² and once again, Q.E.D., the Latin abbreviation for "that which has been demonstrated".
Tomorrow: number theory and Pythagorean Theorem.
Friday, January 25, 2013
The Pythagorean Theorem and its connection to trigonometry.
When teaching math, if I ask a class "What is the Pythagorean Theorem?", invariably someone will eventually pipe up the statement
a² + b² = c²
This is correct as far as it goes, but asking what a, b and c stand for is not always remembered.
Ignoring what names we assign the sides the statement of The Pythagorean Theorem is:
The sum of the squares of the lengths of the legs of a right triangle is equal to the square of the length of the hypotenuse.
Quite often, the phrase "of the length(s)" is removed, since talking about squaring something implies the thing is a number and the number associated with a side of a triangle is the length almost always.
Using the names from the picture above, the equation would change to adj² + opp² = hyp².
So far, so good.
Let's divide all the sides by the hypotenuse.
adj/hyp = cosine
opp/hyp = sine
hyp/hyp = 1
These are still sides of a right triangle with 1 being the hypotenuse, so the equation changes to a form the is the main trigonometric identity sin² + cos² = 1. When I teach the class, I call this The Trigonometric Identity since all the other trig identities are just re-arrangements of this.
Tomorrow, I'll present a proof of the Pythagorean Theorem using basic facts from geometry, the areas of right triangles and the areas of squares.
a² + b² = c²
This is correct as far as it goes, but asking what a, b and c stand for is not always remembered.
Ignoring what names we assign the sides the statement of The Pythagorean Theorem is:
The sum of the squares of the lengths of the legs of a right triangle is equal to the square of the length of the hypotenuse.
Quite often, the phrase "of the length(s)" is removed, since talking about squaring something implies the thing is a number and the number associated with a side of a triangle is the length almost always.
Using the names from the picture above, the equation would change to adj² + opp² = hyp².
So far, so good.
Let's divide all the sides by the hypotenuse.
adj/hyp = cosine
opp/hyp = sine
hyp/hyp = 1
These are still sides of a right triangle with 1 being the hypotenuse, so the equation changes to a form the is the main trigonometric identity sin² + cos² = 1. When I teach the class, I call this The Trigonometric Identity since all the other trig identities are just re-arrangements of this.
Tomorrow, I'll present a proof of the Pythagorean Theorem using basic facts from geometry, the areas of right triangles and the areas of squares.
Thursday, January 24, 2013
The basic trigonometric functions.
If I give you the measure of two interior angles of a triangle, you can figure out the third by adding up the two given numbers and subtracting that number from 180.
In the picture here, the angle on the left is theta degrees and the angle on the lower right is 90 degrees. 180 - (90 + theta) = 90 - theta, which is the measure of the upper right angle.
The two smaller angles must add up to 90 degrees. When two angles have this property, we say the are complementary. Notice, this is different from complimentary, which means saying something nice. Here are the ways to use complementary in a sentence.
30° and 60° are a pair of complementary angles.
30° is complementary to 60° and vice versa.
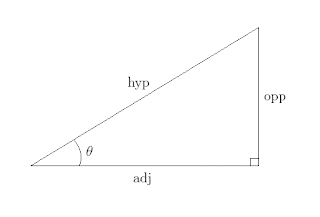
That said, the picture above is an example of a class of similar triangles defined by the three angles, 90°, theta° and (90-theta)°. Just as we have not put a number value to theta, we have not put number values to the lengths of the sides, labeled hyp, opp and adj, respective abbreviations for hypotenuse, opposite and adjacent. We could measure theta exactly and give the measure in degrees, but the numbers for the side lengths would depend on what unit we used. Americans would be likely to measure in inches, most of the rest of the world would use centimeters or millimeters, and some clever computer types might try to figure out the number of pixels in each line as drawn in the computer picture.
If the measurements are exact, the numbers produced will be different but the ratios of matching side lengths should be the same, like the hypotenuse divided by the adjacent or the opposite divided by the hypotenuse. Since we have three numbers, none of which should be zero, we have six different ratios. In trigonometry, there are six basic functions we will associate to an angle measurement, in this case theta.
sine: sin theta = opp/hyp
cosine: cos theta = adj/hyp
tangent: tan theta = opp/adj
cotangent: tan theta = adj/opp (the reciprocal of tangent)
secant: sec theta = hyp/adj (the reciprocal of cosine)
cosecant: csc theta = hyp/opp (the reciprocal of sine)
The prefix "co-" is short for complementary. If we look at the other acute angle (90°-theta), the value for cosine of that angle will be the value for sine of theta, the complementary angle. This is because when we look at the triangle from the point of view of the other angle, the side we had labeled the opposite is now the adjacent and vice versa. The long side is the hypotenuse and it does not change depending on our point of view.
Besides the relationship of complementary values, there are several important trigonometric identities based on The Pythagorean Theorem, which we will discuss tomorrow.
Wednesday, January 23, 2013
Right triangles: Starting with definitions
Nature does not create many straight lines, with the exception of some crystalline forms. Even rarer in nature are right angles, two straight lines meeting like a plus sign + to create four equal angles that add up to 360°, which means every angle created by the two crossing lines of the plus sign measures 90°.
Straight line geometry has been used for several millennia by cultures around the world. When we teach geometry today, it is standard to teach the ideas discovered by the Greeks. For example, the symbol over by the angle on the left of this triangle is the lowercase Greek letter theta. It is a common convention to label angles with Greek letters, points with capital letters from the Roman alphabet and the lengths of straight lines with lowercase letters from the Roman alphabet.
In this picture, we have a right triangle. That little rectangle mark in the lower right hand corner signifies a 90° angle.
The side length opposite the right angle is called the hypotenuse. Since the three angles have a sum of 180°, the 90° angle accounts for half of that and the other two angles must add up to 90°. More than that, there is an easily proved property of triangles that the longest side of any triangle will be opposite the largest angle. Sing the right angle must be the largest angle, the hypotenuse is always the longest side of a right triangle.
The other two sides are called the legs. If we discuss these legs, we often pick one of the smaller angles and distinguish the two legs based on their relation to the chosen smaller angle, which in this case is the one we labeled theta.
The leg that is not on of the line segments next to theta is called the opposite and the leg that creates the angle theta where it intersects with the hypotenuse is called the adjacent.
Tomorrow, we will discuss some of the relationships of the sides and angles of a right triangle using the terms associated with trigonometry.
Tuesday, January 22, 2013
Pascal's Triangle long before Pascal.
Blaise Pascal did not call the array of numbers he studied "Pascal's Triangle". In math, it's considered poor form to name something after yourself.
Pascal's Treatise on the Arithmetic Triangle was published posthumously. In it, he gathered together all the facts he knew about the patterns he discovered himself or had read about in other books. It became the "go to" text for information about the array and other mathematicians started calling it "the triangle of M. Pascal" so much so that it is now the way nearly everyone in the world refers to it.
Nearly everyone. About 100 years before Pascal, the great Italian algebraist Niccolo Fontana, known by his nickname Tartaglia - which means "the stammerer" - did a lot of work with the number pattern and in Italian the array is known as Tartaglia's Triangle.
Several centuries earlier, the Chinese were discovering things about the array, and in Chinese it is known as Yang Hui's Triangle.
But the Chinese from 700 years ago are not the first people to study the numbers and leave a paper trail behind that future generations could find. There are two completely different problems from before the birth of Christ that originate in India whose answers come from the numbers in the array we call Pascal's Triangle.
Let's say we have a spice rack with six flavors: salt, pepper, garlic, nutmeg, curry and basil. How many different combination of three spices are there? (Note: in this problem, we are not saying how much of any one spice we are using, only if it is used. Two parts salt and one part garlic would taste different from one part salt and two parts garlic, but in this problem we would say that both are salt/garlic combinations.)
If we abbreviate the spices to S, P, G, N, C and B, here are the 20 different groups of three
Salt included
SPG SPN SPC SPB
SGN SGC SGB
SNC SNB
SCB
Salt excluded, pepper included
PGN PGC PGB
PNC PNB
PCB
Salt and pepper excluded, ginger included
GNC GNB
GCB
No salt, pepper or ginger
NCB
The other ancient problem from India that uses the binomial coefficients deals with music and rhythm. In the musical notation developed in Europe that is used almost everywhere today, if we say a song is in a rhythm of six beats, all those beats have the same duration. In India, beats can either be short or long. For instance, let's say we had a song that has double hand claps on the second and fourth beat of every measure, so the pattern might the counted out
bump clap-clap bump clap-clap...
In Western music, we would say this is a four beat pattern. In Indian music, they would say it is a six beat pattern.
long short short long short short.
Okay so how many different six beat patterns have three long beats and three short beats? Again the answer is 20.
First beat long
LLLSSS LLSLSS LLSSLS LLSSSL
LSLLSS LSLSLS LSLSSL LSSLLS
LSSLSL LSSSLL
First beat short, second beat long
SLLLSS SLLSLS SLLSSL SLSLLS
SLSLSL SLSSLL
First two beats short, third beat long
SSLLLS SSLLSL
SSLSLL
First three beats short
SSSLLL
At first glance, these problems don't seem to be connected, but in fact they are. If we line up the spices alphabetically in English, we would get.
Basil Curry Garlic Nutmeg Pepper Salt
Take any six beat pattern.
LLSSLS
Think of L as being yes and S as being no
YesYesNoNoYesNo.
Make a spice combination where we only use the spices that correspond to the Yes positions.
Basil Yes, Curry Yes, Garlic No, Nutmeg No, Pepper Yes, Salt No.
In this way, the beat pattern LLSSLS corresponds to the recipe that uses basil, curry and pepper. If two beat patterns are different, they will correspond to different recipes. In math, this kind of matching is called a one to one correspondence, and it is one way to prove that one set of objects has the same number of things as another set.
Tomorrow, we will look at actual geometric triangles, notably triangles with one right angle, known simply enough as right triangles.
Monday, January 21, 2013
The closed factorial form for the binomial coefficients
So far we have learned how to create Pascal's Triangle by using one row to generate the next.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
...
What if we wanted to know how many different five card hands of poker there are. If we care about the suits of the cards, then "four aces and the king of spades" is different from "four aces and the king of clubs". Counting that way the number of cards is "52 choose 5", the number of way to select five cards from a deck of fifty two.
Here is the closed form for the binomial coefficients. If this is the first time you have seen an exclamation point used in math, it means factorial.
n! = n(n-1)(n-2)(n-3)...(3)(2)(1), all the whole numbers from n to 1 multiplied together. Let's do an example from part of the triangle we've already seen.
7 choose 2 is 7!/[2!5!]. notice that the 5×4×3×2×1 shows up in both the numerator and denominator, so it therefore can be cancelled out. We are left with 7×6/(2×1), which is 21.
52 choose 5 will also have a lot of simple cancellations, and we end up with five consecutive numbers in the numerator divided by 5×4×3×2×1. When all the denominator is cancelled out, we are left with 2,598,960.
Tomorrow: Two problems from ancient India solved by numbers from the Triangle.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
...
What if we wanted to know how many different five card hands of poker there are. If we care about the suits of the cards, then "four aces and the king of spades" is different from "four aces and the king of clubs". Counting that way the number of cards is "52 choose 5", the number of way to select five cards from a deck of fifty two.
Here is the closed form for the binomial coefficients. If this is the first time you have seen an exclamation point used in math, it means factorial.
n! = n(n-1)(n-2)(n-3)...(3)(2)(1), all the whole numbers from n to 1 multiplied together. Let's do an example from part of the triangle we've already seen.
7 choose 2 is 7!/[2!5!]. notice that the 5×4×3×2×1 shows up in both the numerator and denominator, so it therefore can be cancelled out. We are left with 7×6/(2×1), which is 21.
52 choose 5 will also have a lot of simple cancellations, and we end up with five consecutive numbers in the numerator divided by 5×4×3×2×1. When all the denominator is cancelled out, we are left with 2,598,960.
Tomorrow: Two problems from ancient India solved by numbers from the Triangle.
Sunday, January 20, 2013
The Hockey Stick Theorem
Earlier, we discussed the pattern from Pascal's Triangle known as the Christmas Stocking Theorem, named for a shape that has a toe and a leg, the leg being a column inside the triangle. Here is an example in bold and blue.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
What this shows is that 20 = 10+6+3+1, the toe of the stocking equal to the sum of the numbers in the leg.
A Hockey Stick will lie flat across a row like this
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Obviously, the 6 in the toe is not the sum of the numbers in the row below. It is the alternating sum, which is to say we start at the 21 just below the 6, then subtract the 35 to the left, then add the next 35, subtract the next 21, add the 7 then subtract the 1. Let me write it this way, with the subtractions written in red.
6 = 21 - 35 + 35 - 21 + 7 - 1
Here is the summation notation of the pattern.
If I were in front of a class, I would say
"n choose r equals the alternating sum of negative one to the r-k power times n+1 choose k as k goes from 0 to r."
Alternating sums always have -1 raised to integer powers, since (-1)(-1) = 1 but (-1)(-1)(-1) = -1, etc. -1 raised to an even power is 1, while raised to an odd power is -1.
Tomorrow, we will learn the closed form of the binomial coefficients, a useful thing to know if we want to find out the different number of five card hands in poker without having to write out rows 0 to 52 of the triangle.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
What this shows is that 20 = 10+6+3+1, the toe of the stocking equal to the sum of the numbers in the leg.
A Hockey Stick will lie flat across a row like this
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Obviously, the 6 in the toe is not the sum of the numbers in the row below. It is the alternating sum, which is to say we start at the 21 just below the 6, then subtract the 35 to the left, then add the next 35, subtract the next 21, add the 7 then subtract the 1. Let me write it this way, with the subtractions written in red.
6 = 21 - 35 + 35 - 21 + 7 - 1
Here is the summation notation of the pattern.
If I were in front of a class, I would say
"n choose r equals the alternating sum of negative one to the r-k power times n+1 choose k as k goes from 0 to r."
Alternating sums always have -1 raised to integer powers, since (-1)(-1) = 1 but (-1)(-1)(-1) = -1, etc. -1 raised to an even power is 1, while raised to an odd power is -1.
Tomorrow, we will learn the closed form of the binomial coefficients, a useful thing to know if we want to find out the different number of five card hands in poker without having to write out rows 0 to 52 of the triangle.
Saturday, January 19, 2013
The sum of the n-th row of Pascal's Triangle is 2 to the n-th power
Yesterday, we proved the statement that is the title of this post. Why prove it again?
Proof in mathematics is vitally important and multiple proofs of the same fact (or theorem) can show different ways things are connected to each other.
The style of proof we see today is called induction. Here is the basic idea.
1. Make a statement about an infinite number of things that you can put in order.
2. Prove it for the first thing.
3. Prove that if it is true for any given thing on the list, it must also be true for the next thing on the list.
The infinite things we are putting in order are the sums of the rows of Pascal's Triangle.
1=1
2=1+1
4=1+2+1
8=1+3+3+1
...
The first thing on the list is the sum of 1 in row 0. 1 = 2º, so that means we have done steps 1 and 2 of induction.
Now I'm going to cheat a little to make things clear. I am going to use the third row of Pascal's Triangle for my next step. I shouldn't use a specific row because induction has to be about any given row. I'm going to cheat here to convince the reader that what happens to go from the third row to the fourth row happens going from any row to the next. I'm going to use four different colors on the four different numbers.
1 3 3 1
next row created by adding numbers from the current row. (0 are in black.)
0+1 1+3 3+3 3+1 1+0
Notice that every color of number shows up exactly twice, two purple 1s, two red 3s, two green 3s and two blue 1s. This means that the sum of this row must be exactly twice the sum of the row we were looking at.
Proving this is true between rows three and four is not enough. You need to convince yourself the pattern of doubling is true between any two consecutive rows. The reason that it's true is that every number in a row is used exactly twice in two different sums to create the entries of the next row.
Tomorrow, we continue to look at patterns in Pascal's Triangle. We have seen the Christmas Stocking, now we will discover the hockey stick.
Friday, January 18, 2013
The sum of the n-th row of Pascal's Triangle is always 2 to the power of n.
Yesterday, we discussed the Binomial Theorem, the standard way to expand a binomial, here expressed as (x + y), raised to any positive integer power n.
We also have a simple pattern easily visible in the first few rows of Pascal's Triangle.
1 = 1
2 = 1+1
4 = 1+2+1
8 = 1+3+3+1
16= 1+4+6+4+1
...
From what we can see, the sum of the n-th row is 2 raised to the power of n. In math, we can't just say we see a pattern for a few rows and assume it is always true, we need to prove it is true. Here is the proof.
Step 1 is no more difficult than 2 = 1+1. Pretty easy.
Step 2 is to take the Binomial Theorem and replace the general binomial (x + y) with the specific binomial (1+1). So we get all the entries of row n multiplied by powers of 1 then added up.
Any integer power of 1 is 1, so we can erase those powers because they are superfluous.
Now we just have the sum across the row. Since the equations are of the form
a = b, then b = c, then c = d, we can also say a = d.
This is not the only way to prove this. Another proof of this basic property of Pascal's Triangle tomorrow.
Thursday, January 17, 2013
The binomial coefficients
The translation of the word binomial means "two names". In algebra, a polynomial is an expression with several terms, a term being a set of numbers and variables multiplied together. The number in the term is called the coefficient. Here are some examples
7xyz² is a single term with three variables. 7 is the coefficient, Since the z is raised to the second power, if we wrote this out in letters it would be 7xyzz, and since we have to used four letters to write this out completely, we say this is a fourth degree term.
7xy - 2z² is two terms, so it is called a binomial. The coefficient of the first term is 7 and the coefficient of the second term is -2.
What happens when we raise a binomial to different powers? Here are the first few examples.
(x + y)º = 1
(x + y)¹ = x + y
(x + y)² = x² + 2xy + y²
(x + y)³ = x³ + 3x²y + 3xy² + y³
If we strip away the variables and just look at the coefficients, we get
1
1 1
1 2 1
1 3 3 1
If you have been reading the blog this week, you know those are the first few rows of Pascal's triangle.
Here is the standard summation form of this fact, usually called The Binomial Theorem.
Notice that the powers for x and y always add up to n when we raise (x + y) to the n-th power.
You might also notice that the sums of the rows of Pascal's Triangle has an easily recognizable pattern.
1 = 1
2 = 1+1
4 = 1+2+1
8 = 1+3+3+1
In these first few cases, it looks like the sum of the n-th row is 2 raised to the power of n. There are many ways to prove this pattern continues forever.
Tomorrow, we will use The Binomial Theorem to prove this pattern.
Wednesday, January 16, 2013
An informal proof of the Christmas Stocking Theorem
Let's put a few rows of Pascal's triangle up yet again and choose one of the entries "at random", providing it isn't in the leftmost column.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
The first rule we have learned about entries in that any entry is the sum of the entry just above it and the entry above it and to the left, in this case, 35+21 = 56.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
I'm going to use the same rule on the 21, changing it to 15+6, the entries above it.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Now the 6, changing it to 5+1, the entries above it.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Now the 1 in row 5 is exchanged for the 1 in row 4, actually 1 = 1+0, but the zero is invisible.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Now I un-bold the 1 in row 5 and we have our standard Christmas Stocking, the sum of the leg in bold red being equal to the toe in bold black.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Here is how I could say the theorem in everyday language.
Pick any column in Pascal's Triangle. Starting at the top of the column, select as many entries as you want and add them up. The sum will be equal to the entry that is one row down and one column to the right of the position where you list of entries ended.
Here is how I would write this in summation notation. The letter k stands for the column, the letter n stands for where we stop counting and the letter j is the summation variable, which goes from k to n.
Here is how I would say this summation out loud if I were explaining it in class.
The sum as j goes from k to n of "j choose k" is "n+1 choose k+1".
The parentheses with two numbers on top of each other is the standard way to write the numbers of Pascal's Triangle, known collectively as the binomial coefficients. The editor that Blogger uses doesn't have an elegant way to put up a summation symbol or stacking numbers inside a parentheses, so I will write "8 choose 5" = 56 when I mention an entry or "j choose k" when discussing a general entry.
Tomorrow: Why the entries are called binomial coefficients.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
The first rule we have learned about entries in that any entry is the sum of the entry just above it and the entry above it and to the left, in this case, 35+21 = 56.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
I'm going to use the same rule on the 21, changing it to 15+6, the entries above it.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Now the 6, changing it to 5+1, the entries above it.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Now the 1 in row 5 is exchanged for the 1 in row 4, actually 1 = 1+0, but the zero is invisible.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Now I un-bold the 1 in row 5 and we have our standard Christmas Stocking, the sum of the leg in bold red being equal to the toe in bold black.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Here is how I could say the theorem in everyday language.
Pick any column in Pascal's Triangle. Starting at the top of the column, select as many entries as you want and add them up. The sum will be equal to the entry that is one row down and one column to the right of the position where you list of entries ended.
Here is how I would write this in summation notation. The letter k stands for the column, the letter n stands for where we stop counting and the letter j is the summation variable, which goes from k to n.
Here is how I would say this summation out loud if I were explaining it in class.
The sum as j goes from k to n of "j choose k" is "n+1 choose k+1".
The parentheses with two numbers on top of each other is the standard way to write the numbers of Pascal's Triangle, known collectively as the binomial coefficients. The editor that Blogger uses doesn't have an elegant way to put up a summation symbol or stacking numbers inside a parentheses, so I will write "8 choose 5" = 56 when I mention an entry or "j choose k" when discussing a general entry.
Tomorrow: Why the entries are called binomial coefficients.
Tuesday, January 15, 2013
The naming convention for Pascal's Triangle.
Yesterday, I wrote down the rules for creating Pascal's Triangle using addition of the row elements above the chosen row element. Here are the values of the first nine rows.
row 0 = 1
row 1 = 1 1
row 2 = 1 2 1
row 3 = 1 3 3 1
row 4 = 1 4 6 4 1
row 5 = 1 5 10 10 5 1
row 6 = 1 6 15 20 15 6 1
row 7 = 1 7 21 35 35 21 7 1
row 8 = 1 8 28 56 70 56 28 8 1
Notice that we call the top row "row 0" instead of "row 1". We do a similar thing when labeling the columns. The left most column, which is filled with the number 1 in every row, is column 0. For example, the 6 in row 4 is "row 4, column 2". Here is a triangle of the labels, where r2c0 is shorthand for "row 2, column 0".
r0c0
r1c0 r1c1
r2c0 r2c1 r2c2
r3c0 r3c1 r3c2 r3c3
r4c0 r4c1 r4c2 r4c3 r4c4
...
The standard way to say the name of a binomial coefficient is "5 choose 2" or "7 choose 3". "5 choose 2" is the first 10 in row 5. "7 choose 3" is the first 35 in row 7.
Here is why that name caught on. Let's say you have five distinct things that you can tell apart. We'll call them a, b, c, d and e. How many different ways are there to choose two of them? If you think of them as cards in a deck, this would be the same as asking how many different two card hands can you make, where ae is considered to be the same as ea. (In most card games, you are allowed to rearrange your hand and the order of the cards in your hand is not essential to the rules of the games.) Here is the list of all the two card hands in alphabetical order, where each hand has the letters in alphabetical order as well.
ab ac ad ae (all the hands where a is the in the hand)
bc bd be (all the hands where b is the first card alphabetically)
cd ce (all the hands where c is the first card alphabetically)
de (all the hands where d is the first card alphabetically)
Counting it this way, we get 4+3+2+1 = 10. As it turns out "n choose 2" is always a triangular number. If you look at column 2 in the Pascal's triangle above, you see 1, 3, 6, 10, 15, 21, 28..., the first seven triangular numbers.
Let me make the list that corresponds to "7 choose 3". Our list of things is now {a, b, c, d, e, f, g}. It wouldn't change anything vital to make the list {1, 2, 3, 4, 5, 6, 7}. Any seven things we can tell apart will do.
Here are all the three letter groups that include a in alphabetical order.
abc abd abe abf abg
acd ace acf acg
ade adf adg
aef aeg
afg
So far, 15 things on the list. Now the three letter groups where b comes first alphabetically.
bcd bce bcf bcg
bde bdf bdg
bef beg
bfg
10 more, the total is now 25. Groups with c as the first letter.
cde cdf cdg
cef ceg
cfg
6 more, total is 31. Groups with d first.
def deg
dfg
3 more, total 34. And one last group where e is the first letter in the group.
efg
The final total is 35. Notice that this says that "7 choose 3" = 35, a number in the third column can be created as a sum of numbers in the second column. Let me mark those numbers in red and bold in this copy of the triangle.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
This leads us to one of the first patterns embedded in Pascal's Triangle, often called The Christmas Stocking Theorem, since the shape looks something like a sock or a boot. In this case the 35 is the toe and the other numbers make up the part that covers the leg.
Tomorrow, I will show a construction style proof that makes it clear the Christmas Stocking Theorem works for any number in the Triangle used as the toe, providing it isn't in column 0, because we need a non-empty column to the left to make this pattern work.
Monday, January 14, 2013
Pascal's Triangle
You may have seen Pascal's Triangle at some time in your education. It is an array of numbers where each row has one more number in it than the last row. The top row is just the number 1 and the second row is 1 and 1, so these rows look like this.
1
1 1
The rule for creating the entries of a row are based on the row just above it. Here is how to state it as a sentence.
An entry in Pascal's Triangle is the sum of the entry just above it in the previous row and the number just above it and to the left. If one of these numbers doesn't exist, assume it is zero.
That means the next row down will be 1(+0), 1+1 and (0+)1 so the first three rows look like
1
1 1
1 2 1
Like the Fibonacci sequence, the numbers go on forever. Here are the first nine rows, which is the last row before the biggest number is more than two digits long.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
The numbers are known as the binomial coefficients and they turn out to be the answers to a remarkable number of different questions about how to count things. The field of counting things in math is called combinatorics. This because it sounds more impressive to say "I study combinatorics" instead of saying "I count things for a living."
All this week we will look at the numbers in Pascal's Triangle and discuss the history how these numbers were used.
Tomorrow: The standard way to identify numbers in the array.
1
1 1
The rule for creating the entries of a row are based on the row just above it. Here is how to state it as a sentence.
An entry in Pascal's Triangle is the sum of the entry just above it in the previous row and the number just above it and to the left. If one of these numbers doesn't exist, assume it is zero.
That means the next row down will be 1(+0), 1+1 and (0+)1 so the first three rows look like
1
1 1
1 2 1
Like the Fibonacci sequence, the numbers go on forever. Here are the first nine rows, which is the last row before the biggest number is more than two digits long.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
The numbers are known as the binomial coefficients and they turn out to be the answers to a remarkable number of different questions about how to count things. The field of counting things in math is called combinatorics. This because it sounds more impressive to say "I study combinatorics" instead of saying "I count things for a living."
All this week we will look at the numbers in Pascal's Triangle and discuss the history how these numbers were used.
Tomorrow: The standard way to identify numbers in the array.
Sunday, January 13, 2013
Sum of two squares and the prime numbers of the form 4k+1
Repeating the definition of prime numbers.
Definition: A prime number p is a positive integer that has exactly two factors, 1 and p itself.
2 is the only even prime. Other small primes include 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37... The list goes on forever as there is no largest prime number.
One way to split up the odd primes is to divide by 4 and check the remainder.
With 3, 4 goes in 0 times with remainder 3.
With 5, 4 goes in 1 time with remainder 1.
With 7, 4 goes in 1 time with remainder 3.
With 11, 4 goes in 2 times with remainder 3.
With 13, 4 goes in 3 times with remainder 1.
With 17, 4 goes in 4 times with remainder 1.
With a little thought, it's easy to convince yourself that the only options for the remainder are 1 and 3, so we can split the odd primes into two camps, the 4k + 1 primes {5, 13, 17, 29, ...} and the 4k + 3 primes {3, 7, 11, 19, 23...}.
Let's look at perfect squares. An even number can always be written 2k, while an odd number can be written as 2k+1. Here's what happens when we square even numbers and odd numbers.
(2k)² = 4k²
(2k+1)² = 4k² + 4k + 1
What this tells us is that even perfect squares are not just divisible by 2, but also divisible by 4. Take a look at 4, 16, 36, 64, 100, 144, etc. if you need convincing.
For the odd squares (1, 5, 9, 25, 49, 81, etc.) you will always get the remainder of 1 when you divide by 4.
Fact with easy proof: No prime of the form 4k + 3 can be the sum of two squares.
Even square + even square = divisible by 4
Even square + odd square = remainder of 1 when dividing by 4
Odd square + odd square = remainder of 2 when dividing by 4
So the sum of two squares when divided by 4 can have remainder 0, 1 or 2, but not 3.
Fact with much harder proof: Every prime of the form 4k + 1 can be written as the sum of two squares and the choice of the two squares, one even and one odd, is unique for each prime.
Let me show you the first few examples.
5 = 2²+ 1² = 4 + 1
13 = 2²+ 3² = 4 + 9
17 = 4²+ 1² = 16 + 1
29 = 2²+ 5² = 4 +25
37 = 6²+ 1² = 36 + 1
41 = 4²+ 5² = 16 +25
This is not an easy proof and beyond the scope of what I want to discuss on the blog. To me, this is one of those remarkable things you can discover in higher mathematics. It's remarkable that it works for every prime of the form 4k+1 and doubly remarkable that the solution is unique for each prime of that form.
Tomorrow: Fun with Pascal's Triangle.
Saturday, January 12, 2013
A pattern within the perfect squares.
The perfect squares are the numbers that are the result of multiplying a whole number by itself.
On Tuesday, we saw that every perfect square is the sum of two consecutive triangular numbers, such as 21 + 15 = 36 = 6², illustrated below with 21 black asterisks (6+5+4+3+2+1) and 15 red asterisks (1+2+3+4+5).
* * * * * *
* * * * * *
* * * * * *
* * * * * *
* * * * * *
* * * * * *
Here is another summation method that gives us the perfect squares, once again illustrated with squares made from asterisks, starting with 1² = 1.
*
2² = 4 = 1 + 3.
* *
* *
3² = 9 = 1 + 3 + 5.
* * *
* * *
* * *
4² = 16 = 1 + 3 + 5 + 7.
* * * *
* * * *
* * * *
* * * *
The most direct way to state this is n² is the sum of the first n odd numbers or n² = 1 + 3 + ... + (2n - 1).
Taking the sum of a pattern of numbers is very common in math, so we took the capital Greek letter sigma as the symbol for summation. Blogger software doesn't have an easy way for me to write sigma correctly, so I will add a picture.
The big thing at the front that looks like an M lying on its side is the sigma. I also introduced a new variable k, which is the counting variable. The symbols above and below the sigma mean "k starts at 1, and increases by 1 each time until it gets to n, then we stop". The (2k - 1) shows the things we are adding together.
When k = 1, then 2(1) - 1 = 1.
When k = 2, then 2(2) - 1 = 3.
When k = 3, then 2(3) - 1 = 5.
When k = 4, then 2(4) - 1 = 7.
etc. ...
Tomorrow: a pattern concerning squares and the prime numbers of the form 4k + 1.
Friday, January 11, 2013
Fibonacci numbers and phi, the golden mean.
The Fibonacci sequence is created by adding things together, which makes it an arithmetic sequence. In this usage of the word, it is pronounced ar-ith-ME-tic instead of ar-ITH-me-tic.
A sequence created by multiplying things together is called a geometric sequence, pronounced exactly as you would expect. For example, the powers of two are geometric.
1
1 × 2 = 2
2 × 2 = 4
4 × 2 = 8
8 × 2 = 16
...
If the Fibonacci sequence was geometric, you would see a clear and simple pattern when you divided a Fibonacci number by the next one in the sequence, but this pattern is neither clear or simple.
1/1 = 1
2/1 = 2
3/2 = 1.5
5/3 = 1.666666...
8/5 = 1.6
11/8 = 1.625
...
Obviously, the numbers change each time. Not quite as obviously, there is a pattern called an alternating sequence. 2 > 1, but 1.5 < 2. The sequence gets bigger, then smaller, then bigger, then smaller, ad infinitum. More than that the small numbers (1, 1.5, 1.6...) are growing and the big numbers (2, 1.666..., 1.625) are shrinking. This means the two sequences are converging. In this particular case, they are converging towards a number called phi (pronounced 'fee'), which is also known as the Golden Ratio, which can be expressed by the algebraic number (1 + sqrt(5))/2, which is approximately 1.61803...
The number phi creates a spiral known as the Golden Spiral. It keeps getting larger by the same ratio and also smaller by the same ratio, a pattern which goes infinitely in either direction, both growing and shrinking.
This spiral is based on the Fibonacci sequence. As it gets bigger and more squares with quarter circles are added, it gets to look more and more like the Golden Spiral, but it does not shrink indefinitely, starting with squares of size 1 ×1, 1 ×1, 2 × 2, 3 × 3, 5 × 5, etc. When I teach this method, I call it the Gold Plated Spiral, but that is not a generally used name.
Tomorrow: Perfect squares and sums of odd numbers.
Thursday, January 10, 2013
Fibonacci numbers in nature.
In yesterday's post, I discussed the Fibonacci sequence, the infinite number sequence that starts
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
A sequence that generates the next number in the line by adding together the two numbers just before it. Leonardo of Pisa introduced the numbers in a completely whimsical problem allegedly based on the reproduction cycles of rabbits.
It sometimes happens in math that a tool needed to solve a problem will already exist, built to work on another earlier problem that was often created just for the sake of the beauty of it. So it is with the Fibonacci sequence.
We are often shown cell growth as a constant splitting process, the number of cells doubling each time a new splitting occurs. This is not always the case, as some cells split unequally, one of the new cells getting all the materials needed to replicate at the next splitting time while the second cell does not have what it takes and instead has to use that time period to grow into a ready cell. Here is an example.
Step 1: Cell splits into ready and unready. (2 cells)
Step 2: Ready splits into ready and unready. The earlier unready grows into ready. (3 cells)
Step 3: The two ready cells split, creating two ready cells and two unready cells. The one unready cell from Step 2 grows into ready. (5 cells, 3 ready, 2 unready.)
...
This kind of growth pattern is seen in many plants. Many flowers naturally grow a Fibonacci number of petals, notably 5, 8, 13 or 21.
This top down view of a pine cone shows the number of spirals emanating from the central point. The number of clockwise spirals is 13, but when counting the counter-clockwise, the pattern is not as tight and the number is only 8. With most browsers, this picture animates to show the two counts. If it doesn't work here, try clicking on this link to go to the original.
Tomorrow, the Fibonacci numbers and the Golden Ratio.
Wednesday, January 9, 2013
Fibonacci numbers
Leonardo of Pisa, known more commonly as Fibonacci, was born in about 1170 and died in 1240. He is considered the greatest mathematician of the Middle Ages in Europe. He greatest lasting contribution is his book Liber Abaci, where he recommended the use of the number system he called The Arab numerals (now known as Hindu-Arabic numbers, the ones we use today) instead of the Roman numerals still used in Europe in his day. But his name survives because of a math puzzle he created, and the series of numbers that answer the puzzle are still called the Fibonacci numbers.
The puzzle went as follows. You have a pair of rabbits. Their breeding cycle is one month. The original pair gives birth to a new pair. The newborn rabbits are too young to breed, but the original pair will produce another pair of rabbits in the next month and the newborn will grow to maturity in a month so they will start breeding. How many pair of rabbits will you have in a year?
Of course, rabbits don't actually breed this way, but let's solve the problem anyway
Beginning of January: 1 pair
Beginning of February: 2 pairs, only 1 fertile
Beginning of March: 3 pairs, only 2 fertile
Beginning of April: 5 pairs, 3 fertile
Beginning of May: 8 pairs, 5 fertile
Beginning of June: 13 pairs, 8 fertile
Beginning of July: 21 pairs, 13 fertile
Beginning of August: 34 pairs, 21 fertile
Beginning of September: 55 pairs, 34 fertile
Beginning of October: 89 pairs, 55 fertile
Beginning of November: 144 pairs, 89 fertile
Beginning of December: 233 pairs, 144 fertile
Beginning of next January: 377 pairs, 233 fertile
This is the beginning of the sequence called the Fibonacci numbers. As you can see, the number of fertile rabbits follows the same pattern as the number of rabbits, just a month behind.
The rule that creates the Fibonacci numbers: The next Fibonacci number is always the sum of the previous two Fibonacci numbers.
The modern way to count them: In number theory today, instead of starting with 1 and 2, the Fibonacci sequence starts with 0 and 1. We can write them this way.
f0 = 0
f1 = 1
f2 = 0+1 = 1
f3 = 1+1 = 2
f4 = 1+2 = 3
f5 = 2+3 = 5
f6 = 3+5 = 8
...
When speaking, I would say "f 6 equals 8" or "the sixth Fibonacci number is 8". There are some interesting number theory patterns in the sequence dealing with divisibility.
Rule: Any two consecutive positive Fibonacci numbers are relatively prime.
Rule: The fifth Fibonacci number is 5, and every fifth number in the sequence is divisible by 5.
f10 = 55 and f15 = 233 + 377 = 610. To test it out for yourself, continue the pattern to find f20 and f25.
The answers are in the comments.
Tomorrow: The Fibonacci sequence shows up in nature.
Tuesday, January 8, 2013
Triangular numbers
We learn the perfect squares in school. Here are the first few starting with 1² = 1.
1² = 1
*
2² =4
* *
* *
3² = 9
* * *
* * *
* * *
4² = 16
* * * *
* * * *
* * * *
* * * *
5² = 25
* * * * *
* * * * *
* * * * *
* * * * *
* * * * *
Another series of numbers base on shape are the triangular numbers. Here are the first five examples starting with 1.
*
1 = 1, the 1st triangular number
*
* *
1+2 = 3, the 2nd triangular number
*
* *
* * *
1+2+3 = 6, the 3rd triangular number
*
* *
* * *
* * * *
1+2+3+4 = 10, the 4th triangular number
*
* *
* * *
* * * *
* * * * *
1+2+3+4+5 = 15, the 5th triangular number
So the n-th triangular number is the sum of the numbers from 1 to n. There are games where these numbers show up, notably the ten pins in bowling and the fifteen balls other than the cue in pool. There are many places where these number show up in math, including the total number of handshakes necessary in a room with n+1 people so that every possible pair of people shakes hands. Let's look at the example with 5 people.
Person #1: Shakes hands with 4 people
Person #2: Already counted the handshake with #1, 3 people left.
Person #3: Already counted the handshakes with #1 and #2, 2 people left.
Person #4: Already counted the handshakes with #1, #2 and #3, 1 person.
Person #5: Already counted all the handshakes.
There is a formula for the n-th triangular number, which is ½[n(n + 1)].
Consider our idea called relatively prime, which we discussed yesterday.
Two consecutive square numbers are always relatively prime, like 4² and 5². This follows from the fact that any two consecutive numbers are relatively prime.
After the first pair of triangular numbers, namely 1 and 3, any two consecutive triangular numbers cannot be relatively prime.
Ignoring 1 and 3, the next pair are 3 and 6, which have 3 in common as a factor.
Next are 6 and 10, which have 2 in common.
Next, 10 and 15 have 5 in common as a factor.
The formula shows us the numbers are ½[n(n + 1)] and ½[(n + 1)(n + 2)]. If n is even, the common factor will be n + 1. If n is odd, the common factor will be ½(n + 1).
The square and triangular numbers have a connection. The sum of two consecutive triangular numbers is always a square.
1 + 3 = 4
3 + 6= 9
6 + 10 = 16
10 + 15 = 25
etc. ...
Here is a picture of 10 + 15 = 25 to give an idea why this always works.
* * * * *
* * * * *
* * * * *
* * * * *
* * * * *
Tomorrow: the Fibonacci numbers.
Monday, January 7, 2013
Relatively prime.
You might recall the idea of reducing fractions to lowest terms from school. I hope these memories are not accompanied by cold sweat or outbursts of obscenity. The name for the concept behind lowest terms is relatively prime.
Definition. Two numbers a and b are relatively prime to each other if their respective prime factorizations have no primes in common.
Let's use the idea in the concept where most people see it first, reducing fractions.
Example 1: 40% is the same as the fraction 40/100. This is obviously not in lowest terms, since both are divisible by 10, so 40/100 = 4/10. This is still not in lowest terms since both are even. 4/10 = 2/5, and 2 and 5 are relatively prime. In fact, both 2 and 5 are prime, which might cause some confusion. Let's do a second example of relatively prime number where neither number is prime.
Example 2: 48% is the same as the fraction 48/100, not a relatively prime pair. Let's reduce to lowest terms.
48/100 = 24/50 = 12/25, which is lowest terms.
12 = 3 × 2 × 2, so it isn't prime.
25 = 5 × 5, also not a prime.
The pair 12 and 25 is an example of a relatively prime pair of numbers where neither number is prime.
Tomorrow: The triangular numbers
Subscribe to:
Posts (Atom)