When teaching math, if I ask a class "What is the Pythagorean Theorem?", invariably someone will eventually pipe up the statement
a² +
b² =
c²
This is correct as far as it goes, but asking what a, b and c stand for is not always remembered.
Ignoring what names we assign the sides the statement of The Pythagorean Theorem is:
The sum of the squares of the lengths of the legs of a right triangle is equal to the square of the length of the hypotenuse.
Quite often, the phrase "of the length(s)" is removed, since talking about squaring something implies the thing is a number and the number associated with a side of a triangle is the length almost always.
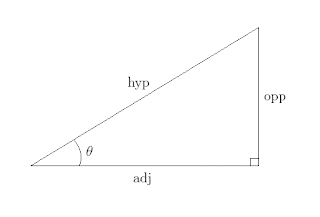
Using the names from the picture above, the equation would change to adj² + opp² = hyp².
So far, so good.
Let's divide all the sides by the hypotenuse.
adj/hyp = cosine
opp/hyp = sine
hyp/hyp = 1
These are still sides of a right triangle with 1 being the hypotenuse, so the equation changes to a form the is the main trigonometric identity sin² + cos² = 1. When I teach the class, I call this The Trigonometric Identity since all the other trig identities are just re-arrangements of this.
Tomorrow, I'll present a proof of the Pythagorean Theorem using basic facts from geometry, the areas of right triangles and the areas of squares.
I appreciate how this post breaks down its historical context and provides clear explanations of the formula. When I first came across this theorem in school, I found it a bit tricky to grasp, but practice really helped. That’s where h2 math tuition plays an important role having someone to guide through concepts like these can make a huge difference. The way you’ve included visual examples in this post is really effective, especially for learners who struggle with abstract mathematical ideas.
ReplyDelete