Sunday, March 31, 2013
The math of space travel
Over on my sci-fi blog, I have printed many of the predictions of Arthur C. Clarke. Some were from novels and stories, others from essays or public appearances where he was asked to look into the future of the next few decades. This week, I printed his prediction that Earth to Saturn would take about seven months, which in his book 2001: A Space Odyssey is done by a manned spacecraft. In reality, we have only sent unmanned craft anywhere farther than our own Moon and the Cassini-Huygens unmanned trip to Saturn took seven years.
Achieving what we consider high speeds in outer space is easier than it is here on Earth. The constraints of friction and gravity are reduced to nearly nothing, so a single burst of propulsion can get a very big result with very little slowing down over time because of drag. One of the problems is slowing down, which will take another big burst of propulsion in the opposite direction. One of the Apollo missions clocked speeds of 25,000 miles per hour. (For my non-Yankee readers, that's about 40,000 kilometers per hour.)
The thing is, in outer space 25,000 mph is not all that fast. To get to Saturn in seven months, you would have to average 150,000 mph.
And then there's interstellar travel, much, much farther away than any of our planets. At those distances, a million miles an hour is pathetically slow. The nearest star that isn't our Sun is about 3,000 years away at a million miles per hour.
Okay, so let's go a billion miles per hour! Then it's less than three years. Well, then we run into another problem that Einstein and others say is insurmountable and that's the speed of light, which is about 670 million miles per hour, or just over one billion kilometers per hour.
Weight has no meaning without gravity, but mass is real regardless. I would weigh less than a toddler on the moon, but I'd still be the same size, the same mass. The thing is, objects gain mass as they go faster, and one of Einstein's theories is that the speed of light is a barrier we can't get past, the increase in mass being so great that the amount of energy needed to go faster would be beyond the limits of anything in the universe. In most of our favorite outer space sci-fi movies and TV shows, there are some tricks that can be pulled to get around this barrier and go faster than light speed, but this is more fiction than science. William Shatner, the actor known best as Captain Kirk, is fond of saying Star Trek is science fiction and Star Wars science fantasy. But both of those fictional universes (and so many others) rely on space travel being possible because of faster than light speeds, a nut that we may never be able to crack.
(Sorry to be such a buzzkill. Happy Easter and enjoy the Games of Thrones season premiere this evening.)
Friday, March 29, 2013
Are all mathematicians crazy?
(This post is an edited version of something I first published in 2007 on my original blog Lotsa 'Splainin' 2 Do.)
When answering the question which is the title of this post, there are two possible answers.
Answer 1: "All mathematicians? All? No, not all mathematicians are crazy."
Answer 2: "Define crazy."
This Rasputin lookin' individual is Grigori Perelman, known to his friends, if any, as Grisha. Grisha is currently unemployed and lives at home with his mom in Saint Petersburg, Russia. A few years back, Grisha gave a talk and published a paper that proved the Poincaré Conjecture was true, gaining worldwide fame in the math community, as well as some headlines out in the real world.
The Poincaré Conjecture is a big damn deal in math. Henri Poincaré, who would be a consensus pick among mathematicians as one of the ten greatest of all time, made this conjecture over a century ago. Lots of smart folks thought a long time about how to prove the statement true.
Grisha actually did it.
Here comes the crazy part. Solving the Poincaré Conjecture comes with a prize of... $1,000,000! (Put your pinky finger to your mouth like Dr. Evil if you feel so inclined.)
Grisha doesn't want it.
Separate from that cash, Grisha has been awarded the Fields Medal, equivalent to the Nobel Prize in math, which also comes with a nice clump of cash. (There is no Nobel Prize in math.)
Grisha doesn't want it.
Maybe his mama could talk some sense into this boy. But taking a good look at him, if she could talk sense into him, she'd probably start by not dressing him funny anymore.
Here is a vague explanation of the Poincaré Conjecture.
In this picture, we have three different objects, a sphere, a torus and a Klein bottle. We are going to consider only the surface of each, which we can think of as a two dimensional thing in a three dimensional world.
The sphere is the easiest of these. It splits the three dimensional world into three parts: the inside of the sphere, (known as a ball), the skin of the sphere and the outside.
A torus is the next easiest. There is an inside, the skin and the outside, but there's the "hole in the middle", which makes a torus different from a sphere in mathematically important ways.
Then we have the physically impossible model that is the Klein bottle. It can be thought of as two Möbius strips glued together along their respective edges. It has to pass through itself in three dimensions without their actually being a hole, which is the impossible part. It has no inside or outside, just like a Möbius strip doesn't have two sides. Mathematicians call a shape like the Klein bottle non-orientable.
Now we get back to the conjecture. All the things up there are two dimensional things embedded in three dimensions. Poincaré was looking at a category of three dimensional objects embedded in four dimensions, and he speculated that all the things in the category were "like" the sphere is in three dimensions. Nice and orientable, no holes like a torus. As simple as things can get in four dimensions.
Lots of people tried to prove it.
Grisha did it.
Now if we just get him to pick up that pile of money with his name on it.
When answering the question which is the title of this post, there are two possible answers.
Answer 1: "All mathematicians? All? No, not all mathematicians are crazy."
Answer 2: "Define crazy."
This Rasputin lookin' individual is Grigori Perelman, known to his friends, if any, as Grisha. Grisha is currently unemployed and lives at home with his mom in Saint Petersburg, Russia. A few years back, Grisha gave a talk and published a paper that proved the Poincaré Conjecture was true, gaining worldwide fame in the math community, as well as some headlines out in the real world.
The Poincaré Conjecture is a big damn deal in math. Henri Poincaré, who would be a consensus pick among mathematicians as one of the ten greatest of all time, made this conjecture over a century ago. Lots of smart folks thought a long time about how to prove the statement true.
Grisha actually did it.
Here comes the crazy part. Solving the Poincaré Conjecture comes with a prize of... $1,000,000! (Put your pinky finger to your mouth like Dr. Evil if you feel so inclined.)
Grisha doesn't want it.
Separate from that cash, Grisha has been awarded the Fields Medal, equivalent to the Nobel Prize in math, which also comes with a nice clump of cash. (There is no Nobel Prize in math.)
Grisha doesn't want it.
Maybe his mama could talk some sense into this boy. But taking a good look at him, if she could talk sense into him, she'd probably start by not dressing him funny anymore.
Here is a vague explanation of the Poincaré Conjecture.
In this picture, we have three different objects, a sphere, a torus and a Klein bottle. We are going to consider only the surface of each, which we can think of as a two dimensional thing in a three dimensional world.
The sphere is the easiest of these. It splits the three dimensional world into three parts: the inside of the sphere, (known as a ball), the skin of the sphere and the outside.
A torus is the next easiest. There is an inside, the skin and the outside, but there's the "hole in the middle", which makes a torus different from a sphere in mathematically important ways.
Then we have the physically impossible model that is the Klein bottle. It can be thought of as two Möbius strips glued together along their respective edges. It has to pass through itself in three dimensions without their actually being a hole, which is the impossible part. It has no inside or outside, just like a Möbius strip doesn't have two sides. Mathematicians call a shape like the Klein bottle non-orientable.
Now we get back to the conjecture. All the things up there are two dimensional things embedded in three dimensions. Poincaré was looking at a category of three dimensional objects embedded in four dimensions, and he speculated that all the things in the category were "like" the sphere is in three dimensions. Nice and orientable, no holes like a torus. As simple as things can get in four dimensions.
Lots of people tried to prove it.
Grisha did it.
Now if we just get him to pick up that pile of money with his name on it.
Thursday, March 28, 2013
A failed experiment - step by step
.
After I finished with the four weeks of climate data, I hoped to make some headway on removing the noise from the temperature data to make the trends easier to see.
This data is the average Winter temperature in Greenland from 1969 to 2010.
The dotted line shows the average of the averages. The first half of the data would be 1969-1989, the second half 1990-2010. It's easy to see the second half has more above average data than the first half.
A different way to measure things is the trendline, also known as the line of correlation or the best fitting line. There are two equations in the picture as well. Let me explain the constants.
0.0507 is the slope of the line. This means that if the rate continued into the future - and we can not assume it will - the temperature is increasing at about one degree every twenty years. That's pretty fast.
The -99.019 would be the temperature if the trendline line were taken back to 1 B.C. As I teach my statistics students, YOU ARE NOT SUPPOSED TO DO THAT! The notice that the trendline is a line segment that doesn't continue either into the future or the past of the time period we decided to look at. Any methods for modeling future behavior have to be a lot more sophisticated than a trendline.
The 0.07203 is the correlation coefficient R². R² is always a number between 0 and 1, and the closer it is to 1, the more confident we are that the line tells us important information about the data. 0.07203 is not close to 1. Even with a data set with 42 points, the lowest R² that makes us 95% confident about what we can say is 0.0973.
Okay, the data isn't really close to linear. We can see that ourselves. The reason I chose the years 1969 and 2010 is that those were peak years of the Atlantic Oscillation, the change in ocean temperatures that should have the most impact on Greenland temperature data.
As you can see, the Atlantic Oscillation is puny compared to the changes in average Winter temperatures in Greenland. Be that as it may, let's factor them out to see what difference that makes.
The green line is the blue line - average - red line. I subtracted the average just so the two lines wouldn't be right on top of each other. As you can see, factoring the oscillation out was not much change.
And now the trendline. Again, the constant -80.798 in the trendline equation is not important, but the slope of 0.0407 and the R² or 0.04628 are important. The slope says that upward movement is slower, only increasing a degree in 25 years instead of 20. (Note: Scientists agree than a degree in 50 years is fast, possibly catastrophic. Either of these speeds is a cause for concern.)
The more important number is R² which shrunk from about 0.072 to 0.046. If correlation had gone up enough to create 95% confidence, I would have considered that I was on the right track. But this experiment didn't work very well and it was not the only one. Other seasons also showed more variation instead of less when the Oscillation was factored out Working with the stronger El Niño/La Niña oscillations on the data of a place like tropical India did not bring the correlation up.
I will continue to look at climate data and will occasionally present data on areas based on similarities of weather rather than just arbitrary longitude and latitude lines. I'm going to see if I can find a climate scientist who has time to talk about this stuff. But subtracting out the oscillations of ocean currents was a promising lead that turned out to be a dead end.
Stuff like that happens when you do research.
After I finished with the four weeks of climate data, I hoped to make some headway on removing the noise from the temperature data to make the trends easier to see.
This data is the average Winter temperature in Greenland from 1969 to 2010.
The dotted line shows the average of the averages. The first half of the data would be 1969-1989, the second half 1990-2010. It's easy to see the second half has more above average data than the first half.
A different way to measure things is the trendline, also known as the line of correlation or the best fitting line. There are two equations in the picture as well. Let me explain the constants.
0.0507 is the slope of the line. This means that if the rate continued into the future - and we can not assume it will - the temperature is increasing at about one degree every twenty years. That's pretty fast.
The -99.019 would be the temperature if the trendline line were taken back to 1 B.C. As I teach my statistics students, YOU ARE NOT SUPPOSED TO DO THAT! The notice that the trendline is a line segment that doesn't continue either into the future or the past of the time period we decided to look at. Any methods for modeling future behavior have to be a lot more sophisticated than a trendline.
The 0.07203 is the correlation coefficient R². R² is always a number between 0 and 1, and the closer it is to 1, the more confident we are that the line tells us important information about the data. 0.07203 is not close to 1. Even with a data set with 42 points, the lowest R² that makes us 95% confident about what we can say is 0.0973.
Okay, the data isn't really close to linear. We can see that ourselves. The reason I chose the years 1969 and 2010 is that those were peak years of the Atlantic Oscillation, the change in ocean temperatures that should have the most impact on Greenland temperature data.
As you can see, the Atlantic Oscillation is puny compared to the changes in average Winter temperatures in Greenland. Be that as it may, let's factor them out to see what difference that makes.
The green line is the blue line - average - red line. I subtracted the average just so the two lines wouldn't be right on top of each other. As you can see, factoring the oscillation out was not much change.
And now the trendline. Again, the constant -80.798 in the trendline equation is not important, but the slope of 0.0407 and the R² or 0.04628 are important. The slope says that upward movement is slower, only increasing a degree in 25 years instead of 20. (Note: Scientists agree than a degree in 50 years is fast, possibly catastrophic. Either of these speeds is a cause for concern.)
The more important number is R² which shrunk from about 0.072 to 0.046. If correlation had gone up enough to create 95% confidence, I would have considered that I was on the right track. But this experiment didn't work very well and it was not the only one. Other seasons also showed more variation instead of less when the Oscillation was factored out Working with the stronger El Niño/La Niña oscillations on the data of a place like tropical India did not bring the correlation up.
I will continue to look at climate data and will occasionally present data on areas based on similarities of weather rather than just arbitrary longitude and latitude lines. I'm going to see if I can find a climate scientist who has time to talk about this stuff. But subtracting out the oscillations of ocean currents was a promising lead that turned out to be a dead end.
Stuff like that happens when you do research.
Wednesday, March 27, 2013
Geometric mean and compound interest
Let's say a report comes out that the growth of the Gross Domestic Product was 4.8% last quarter. Technically, quarterly reports give the annual rate of growth, what would happen if the same growth rate was seen for four consecutive quarters. How do we find the quarter to quarter growth. The simplest answer would be to divide, 4.8%/4 = 1.2%. This is actually a little high.
1.2% quarterly growth means you take what you had and multiply by 101.2%, which is to say the 100% is what you had last quarter and the 1.2% is the amount of growth this quarter. Instead of adding 1.2% every quarter, the correct method would be to raise 101.2% to the fourth power.
1.012 × 1.012 × 1.012 × 1.012 = 1.0488709...
Rounded to the nearest tenth of a percent, this would be 4.9%. It's a small difference, but it is noticeable in the long run. The standard name for this is compound interest.
The correct method to find the quarter to quarter growth rate is to take the fourth root of 1.048, which is 1.011789855... The difference here is small and if we round to the nearest tenth of a percent, we would still get 1.2%. We have to round to one more place to see the rate is closer to 1.18%.
The differences get more noticeable as we use more numbers. Let's look at GDP data from two countries that were hit hard by last decade's financial crisis.
Here are Ireland's quarterly GDP numbers once things start going bad in 2008.
-0.4%, -0.9%, 0.4%, -7.4%, -6.2%, -4.8%, -6.3%, -4.5%, -2.7%, -1.4%, 1.0%, 0.2%, -0.9%, 2.9%, 1%, 2.8%, 2.7%, 0.2%, 0.9%, 0%
Long lists of numbers like this are hard to read and understand and even the chart doesn't tell the whole story. If we add the numbers up and take the average, the Irish economy contracted about 1.17% a year for five years. The correct method is to add 100% to each of these numbers take the fourth root, multiply those together and take the fifth root, since we are looking the five years from the start of 2008 to the beginning of 2013. Using this method, the annual contraction is about 1.22%.
Iceland was another country that took a big hit when the global economy fell. Both Iceland and Ireland were visited by Michael Lewis when he wrote the articles that became the book Boomerang. (He also visited Greece, Germany and California.) Here are the Icelandic GDP numbers over the same time period.
4.8%, 2%, -0.8%, -0.7%, -5.9%, -6.1%, -6.5%, -8.6%, -6.6%, -6.2%, -3.2%, -0.1%, 3.9%, 2.1%, 3.5%, 2.1%, 4.2%, -1.2%, 2.2%, 1.4%
The numbers in Iceland show contraction as well. Done the incorrect way of taking averages, Iceland's economy has contracted at a rate of 0.985%. Doing the geometric mean instead, the annual contraction is 1.07%.
Notice that the correct contraction rates are bigger using geometric means, but a larger contraction actually means a smaller number. This is in line with yesterday's post that geometric means will be less than arithmetic means. In Ireland, it's 98.83% using average and 98.78% using geometric mean. In Iceland, it's 99.015% using average and 98.93% using geometric mean.
Paul Krugman uses Iceland and Ireland as examples to prove austerity doesn't work. After five years, we see only small differences between GDP contraction, so neither can be seen as a miracle or a disaster by this metric.
The major difference is in the unemployment rate. Before things fell apart, the Irish unemployment rate was 4.7%. It has climbed to about 15% and has changed very little. The last data I could find reported in a quick search was 14.2% last November.
Iceland unemployment rate was a much lower 2.4% when the crash hit and climbed to 7.9% at its worst in February 2011. Since then it has fallen and is reported at 5.3% as of last November.
Ireland chose austerity and the people are still paying for it. Iceland forgave a lot but not all of the debt incurred by people who took on mortgages they could not afford. More than that, bank officials and corrupt politicians were aggressively prosecuted in Iceland, several of them now languishing in jail. The Icelandic economy is not all the way back to normal, but it is showing signs of improvement for working people that the Irish method cannot yet show.
Note: when taking averages of unemployment rates, the arithmetic mean is perfectly acceptable. There is no need to factor in any compound interest in these rates.
Tuesday, March 26, 2013
The arithmetic and geometric means
You very well might remember the method for taking an average from your schooling, no matter how long ago that was. If you have a list of numbers and we call the length of the list n, the average is the sum of the numbers divided by n.
The other name for average in math is arithmetic mean. When used as an adjective, it is pronounced a-rith-MET-ic instead of a-RITH-met-ic. In math, a "mean" is a number that lies somewhere in between the highest and lowest number on a list.
Let us look at the arithmetic mean in relation to another mean, the geometric mean. The simplest means to take are when we only have two numbers on our list. For the average, a and b can be any two numbers but the geometric mean is most useful when both the numbers are positive.
We already know that the average of a and b is (a + b)/2 or ½(a + b). The geometric mean of two numbers is the square root of their product, which I will write here as sqrt(ab). One way to think of the geometric mean is to have a rectangle with sides a and b. A square whose sides are the geometric mean has the same area as the rectangle.
Still dealing with positive numbers, if a = b, then the arithmetic mean is equal to the geometric mean. If they are not equal, then the arithmetic mean will be greater than the geometric mean. There are several ways to prove this. This diagram is one of them.
We first put two line segments of lengths a and b next to each other so the total length is a + b. The average is the midpoint of the long line segment. If we draw a half circle with the average as the radius from the midpoint and draw a perpendicular from the point where the a segment and b segment meet, we can make a right triangle where the hypotenuse length is the average (a + b)/2.
The horizontal leg of the right triangle is a - (a + b)/2 = (a - b)/2. Since it's a right triangle we know the some of the squares of the legs equals the square of the hypotenuse, and with a little algebraic manipulation we get this.
[(a + b)/2]² = [(a - b)/2]² + leg² (write the squares out)
(a² + 2ab + b)²/4 = (a² - 2ab + b)²/4 + leg² (subtract the a² and b² out from both sides)
2ab/4 = - 2ab/4 + leg² (add 2ab/4 to both sides and simplify 4ab/4)
ab = leg² (square root of both sides)
sqrt(ab) = leg
The leg of a right triangle must be less than the hypotenuse and that completes our proof in the case where we have two numbers on our list. It is also true when there are more than two numbers on the list, but the proofs become less visual.
Tomorrow, an application of the geometric mean.
Sunday, March 24, 2013
The Atlantic Oscillation Data
Okay, I'll admit it. You are watching someone teaching themselves as much about climate data as they can on their own day by day. Yesterday, I wanted to see about the effect of La Niña and El Niño in the Indian/Pacific Oceans and the effect in the Atlantic.
Silly me. The Atlantic has its own oscillation.
The graph here is the Atlantic oscillation from 1948 to 2012. It is slower and smaller than the La Niña/El Niño changes, only making about a half degree plus or minus in any season at most, compared to about two degree change for La Niña and El Niño at their most severe. The smaller changes take decades to swing back and forth, while La Niña and El Niño can switch from high to low to high again in about ten years.
In any case, this new information means I have to do a little programming to deal with the new data. As the Gosh Darned Pater Familias is fond of saying, you learn something new every day if you are not careful.
Silly me. The Atlantic has its own oscillation.
The graph here is the Atlantic oscillation from 1948 to 2012. It is slower and smaller than the La Niña/El Niño changes, only making about a half degree plus or minus in any season at most, compared to about two degree change for La Niña and El Niño at their most severe. The smaller changes take decades to swing back and forth, while La Niña and El Niño can switch from high to low to high again in about ten years.
In any case, this new information means I have to do a little programming to deal with the new data. As the Gosh Darned Pater Familias is fond of saying, you learn something new every day if you are not careful.
Saturday, March 23, 2013
A new (to me) climate data idea.
As I have stated earlier, the effects of the warming and cooling of vast regions of the Indian and Pacific Oceans near the equator are a very big part of climate in a large area of the world. Any northern Californian who pays attention to weather has heard about La Niña and El Niño as the cause of dry or wet years and we are near the middle of the Norther Temperate zone.
The messy chart presented here, which can be clicked on to show a larger version, shows the effect of the ocean temperatures from 1955 to 2010 through all four seasons each year, as seasons are counted in the northern hemisphere. The thick blue line with empty squares as the markers show the Winter variance from normal, just as green dotted line (circles) shows Spring, the line red line with Xs shows Summer and the thin orange line with diamonds shows Fall.
The idea is to look at regions with this data factored out to see if the pattern gets less variable. We will test "less variability" both visually and with the R² variable from statistics, which shows how much a data set wanders from a regression line. My first test cases will be tropical India, which we would expect will become much less variable being so close to the weather anomaly, and Greenland, which is far from the equator and not bordering the Indian or Pacific Oceans at all.
Friday, March 22, 2013
Four weeks of climate data:
Southern Temperate Temperature Recap
Here is the last of the regions of the world we are looking at, the southern hemisphere's temperate zone. It can be said there is little rhyme or reason in which regions show the most warming compared to northern or southern neighbors. To the south, it's the section of Antarctica south of South America that's burning up, but Chile, Argentina, most of Uruguay and southern Brazil don't show a huge increase. To the north, the tropical South Pacific shows the most warming, but the temperate South Pacific is not warming significantly.
With the exception of Western Antarctica, with its shrinking ice shelves and seriously warming regions, the story of South vs. North can be said simply.
Less land and more ocean, less people, less oceanic ice and less warming.
Tomorrow, we look at the possibility of factoring out the effects of La Niña and El Niño from climate data.
With the exception of Western Antarctica, with its shrinking ice shelves and seriously warming regions, the story of South vs. North can be said simply.
Less land and more ocean, less people, less oceanic ice and less warming.
Tomorrow, we look at the possibility of factoring out the effects of La Niña and El Niño from climate data.
Thursday, March 21, 2013
Four weeks of climate data:
Southern Tropics Temperature Recap
As a general rule, it would be fair to say that the most extreme warming is happening in the Arctic Circle and Western Antarctica. The Western Antarctic warm zone doesn't seem to be radiating out much heat to nearby areas, which is not surprising when you see how far away anything "nearby the Antarctic really is and when you consider the harsh seas and skies that surround the South Pole.
The Southern Tropics have no slice that gets near our somewhat arbitrary level of 1° C rise in temperature over the 56 year period we have chosen to look at, based on Strong La Niña currents.
Tomorrow, our last region, the southern temperate zone, with even more water and less land mass than the southern tropics.
The Southern Tropics have no slice that gets near our somewhat arbitrary level of 1° C rise in temperature over the 56 year period we have chosen to look at, based on Strong La Niña currents.
Tomorrow, our last region, the southern temperate zone, with even more water and less land mass than the southern tropics.
Four weeks of climate data: Northern Tropics Temperature Recap
Because there is less land mass and more ocean, I split the regions other than the Northern Temperate Zone into six sections instead of twelve. As you can see, only the section including Africa and Arabia are showing significant warming. I think it makes sense for me to do some more region testing based on specific areas that are defined by climate and ecosystem, and the Sahara is certainly one of those regions.
The last two slices of the planet, the Southern tropic and Temperate Zones, will be recapped tonight and tomorrow.
The last two slices of the planet, the Southern tropic and Temperate Zones, will be recapped tonight and tomorrow.
Wednesday, March 20, 2013
Four weeks of climate data:
Northern Temperate Western Hemisphere Temperature Recap
The Western Hemisphere of the Northern Temperate Zone doesn't have as much land or as many people as the Eastern Hemisphere of the same zone, and the temperatures aren't as quite as warm. Still, the region is warming noticeably over the 56 year period, in this case only using grid points that have reports from 90% of the seasons between Winter 1955 and Fall 2010.
Tomorrow, I will continue the trip south through both tropical zones. On Friday, I will finish with the Southern Temperate Zone.
I'm working on a new idea of how to look at the data which I call De-Niñoization. The idea is to subtract the El Niño-La Niña effects from each season to see if the data fits a linear regression better. My guess is that we could see improvement in regions close to the temperature anomaly which spreads across the Indian and Pacific Oceans, radiating in strength from close to the equator, but likely less helpful when we look at regions far from the warming water. My test case will be tropical India vs. Greenland, where we would expect the Indian data to become very nearly linear while the Greenland data might become even more erratic.
Tomorrow, I will continue the trip south through both tropical zones. On Friday, I will finish with the Southern Temperate Zone.
I'm working on a new idea of how to look at the data which I call De-Niñoization. The idea is to subtract the El Niño-La Niña effects from each season to see if the data fits a linear regression better. My guess is that we could see improvement in regions close to the temperature anomaly which spreads across the Indian and Pacific Oceans, radiating in strength from close to the equator, but likely less helpful when we look at regions far from the warming water. My test case will be tropical India vs. Greenland, where we would expect the Indian data to become very nearly linear while the Greenland data might become even more erratic.
Four weeks of climate data:
Northern Temperate Eastern Hemisphere Temperature Recap
I changed the method of accepting data for this recap. Previously, if a grid point on my map reported 75% of the time, I considered it reliable and added it to total from which the averages were taken. I saw this was a problem in some of the very sparsely covered regions, like the Indian Ocean region that only had two islands reporting, one much warmer than the other. Today, I re-sampled the data for the Northern Temperate Zone and increased the reporting threshold to 90% of the time. This increased the temperature readings in some regions, decreased it in others, and evened the data out considerably. The number represents the difference in the median of the era 1999-2010 and the era 1955-1975. The years are chosen because all of them were strong La Niña years.
With these readings, the consensus is clear. This region, easily the most populous in the world, went up about a degree Celsius over a 56 year time span, 1955-2010. I am not certain why the second section shows so much more warming than the rest. I'll split it up into smaller parts to see if the north or the south is making the difference.
According to climatologists, the unexploded time bomb in this region is a permafrost located in Siberia, some of it in the Arctic and some in the temperate. "Perma" is relative, but this particular chunk has been ice for about 10,000 years and covers an area equal to France and Germany combined. If this melts, and it has started, the effect is not just albedo (frost reflects heat, land absorbs more) but the amount of carbon dioxide that will be released as the ice becomes water and the bubbles trapped in the ice are released into the atmosphere.
To be clear, this region is not warming at the pace of the Arctic Circle, but it is warming consistently if we look at the data from the most consistently reporting weather stations. Later today, we will look at the numbers from the Western Hemisphere, again relying on the grid points that report at least 90% of the time.
Tuesday, March 19, 2013
Four weeks of climate data:
Antarctica Temperature Recap
What do the numbers mean? These are the increases in the median temperatures Celsius from the 1955-1975 era to the 1999-2010 era in these six slices of the Antarctica out to 60° South Latitude. That gives as all the Antarctic Peninsula and adds no part of any other continent.
Why the question marks? Using the methodology below of only using grid points with at least 90% of the seasons between 1955 and 2010 reporting, the slice south of Africa and the slice directly opposite had no readings at all.
Why those years? All four of those years are strong La Niña years.
What's the methodology? Splitting each slice into a 10 × 10 grid and looking for grid points that reported temperatures in at least 90% of the seasons between 1955 and 2010.
Are these numbers big or small? They are all over the place. The rise of 1.92° C and 2.77° C in the two regions surrounding the Antarctic Peninsula are very large indeed, as is the -1.17° C drop in the region south of the Indian Ocean. There isn't another region in the ones we chose that had a drop that steep.
What's the cause? In the two slices with big increase, the change is albedo, areas where ice on the sea surface melts and exposes more water. Losing oceanic ice does NOT increase sea level, but it does mean more heat is absorbed. This is a feedback loop.
As for the region getting cooler, this may be due to more sea ice than before.
What's the main problem? Melting ice caps in the land mass around the Antarctic Peninsula.
What do humans have to do with this? Once again, greenhouse gases.
For answers to more questions, check out the Arctic recap.
Tomorrow, the temperate zone of the Northern Hemisphere, by far the most populous zone and the most land mass, so it is split into twelve slices instead of just six.
Four weeks of climate data:
Arctic Circle Temperature Recap
It's time for a visit from my blog partner, Hypothetical Question Asker.
What do the numbers mean? These are the increases in the median temperatures Celsius from the 1955-1975 era to the 1999-2010 era in these six slices of the Arctic Circle.
Why those years? All four of those years are strong La Niña years.
What's the methodology? Splitting each slice into a 10 × 10 grid and looking for grid points that reported temperatures in at least 90% of the seasons between 1955 and 2010.
Are these numbers big or small? These numbers are hella big, as we say in Oakland. One degree in 56 years is a Big Damn Deal and the smallest number here is 1.38° C.
What's the cause? In most of the slices, the big change is albedo, areas where ice on the sea surface melts and exposes more water. Losing oceanic ice does NOT increase sea level, but it does mean more heat is absorbed. This is a feedback loop.
What's the main problem? Melting ice caps in the land mass close to the pole, most notably Greenland but also the northernmost islands of Canada.
What do humans have to do with this? Greenhouse gases are our main contribution to the mix as far as the Arctic is concerned. Carbon dioxide (CO2), which is measured in parts per billion in the atmosphere, is at an unprecedented level. The thing is, the earth's climate is a very big thing that doesn't evenly distribute anything.
If CO2 levels are higher than ever, why aren't temperatures higher than ever? That is a fair question. Not every system increases linearly. For example, gravity increases linearly when mass is increased, but decreases by the reciprocal of the square when distance increases. Other systems only increase by the square root or fourth root of some important variable. The greenhouse gas model hasn't been pushed to this level before, so maybe we will find out a linear increase isn't in the cards. In this case, slower would be better.
Is global warming to blame for Katrina or Sandy or the droughts in the Midwest? Here, the predictive model doesn't state that exactly. The most that climate scientists can say is the odds of certain things happening seem to be on the rise and that rise is definitely noticeable. For example, there are events called "100 year storms", based on the idea they can be expected to happen every 100 years. In some parts of the globe, the odds of the "100 year storm" have increased so much that they might now be fairly called "10 year storms" or even "5 year storms".
Later today, a similar recap for Antarctica.
What do the numbers mean? These are the increases in the median temperatures Celsius from the 1955-1975 era to the 1999-2010 era in these six slices of the Arctic Circle.
Why those years? All four of those years are strong La Niña years.
What's the methodology? Splitting each slice into a 10 × 10 grid and looking for grid points that reported temperatures in at least 90% of the seasons between 1955 and 2010.
Are these numbers big or small? These numbers are hella big, as we say in Oakland. One degree in 56 years is a Big Damn Deal and the smallest number here is 1.38° C.
What's the cause? In most of the slices, the big change is albedo, areas where ice on the sea surface melts and exposes more water. Losing oceanic ice does NOT increase sea level, but it does mean more heat is absorbed. This is a feedback loop.
What's the main problem? Melting ice caps in the land mass close to the pole, most notably Greenland but also the northernmost islands of Canada.
What do humans have to do with this? Greenhouse gases are our main contribution to the mix as far as the Arctic is concerned. Carbon dioxide (CO2), which is measured in parts per billion in the atmosphere, is at an unprecedented level. The thing is, the earth's climate is a very big thing that doesn't evenly distribute anything.
If CO2 levels are higher than ever, why aren't temperatures higher than ever? That is a fair question. Not every system increases linearly. For example, gravity increases linearly when mass is increased, but decreases by the reciprocal of the square when distance increases. Other systems only increase by the square root or fourth root of some important variable. The greenhouse gas model hasn't been pushed to this level before, so maybe we will find out a linear increase isn't in the cards. In this case, slower would be better.
Is global warming to blame for Katrina or Sandy or the droughts in the Midwest? Here, the predictive model doesn't state that exactly. The most that climate scientists can say is the odds of certain things happening seem to be on the rise and that rise is definitely noticeable. For example, there are events called "100 year storms", based on the idea they can be expected to happen every 100 years. In some parts of the globe, the odds of the "100 year storm" have increased so much that they might now be fairly called "10 year storms" or even "5 year storms".
Later today, a similar recap for Antarctica.
Monday, March 18, 2013
Four weeks of climate data:
Southern Temperate Region #6
The last region is the temperate section of the South Atlantic.
Just so we are clear, temperate islands are NOT tropical islands, and ten degrees of latitude can make a huge difference. It's cool in Tristan de Cunha and COLD in the South Georgia Islands.
A few years were taken out because only one island or the other was reporting. Taken together the Summer temperature jumped over a degree, which is definitely to be noticed.
On the other hand, the Fall median barely moved, though the record highs and lows did show a big jump.
In the Winter data, both the record high and median more of less flatline.
Spring shows increase in the high and median.
Confidence of the region warming:90.8%
Confidence of increasing rate: 79.2%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.46° C
We are not 95% confident the trend is warming here and the median composite rose less than a half degree Celsius in 56 years, which is not a serious cause for alarm.
This is the last region to look at in our Four Weeks of Climate Data, so now we will go into recap mode, looking at what regions are showing serious increases of more than a degree C from 1955-2010 and which ones are not warming as fast, starting with our six slices of the Arctic.
Just so we are clear, temperate islands are NOT tropical islands, and ten degrees of latitude can make a huge difference. It's cool in Tristan de Cunha and COLD in the South Georgia Islands.
A few years were taken out because only one island or the other was reporting. Taken together the Summer temperature jumped over a degree, which is definitely to be noticed.
On the other hand, the Fall median barely moved, though the record highs and lows did show a big jump.
In the Winter data, both the record high and median more of less flatline.
Spring shows increase in the high and median.
Confidence of the region warming:90.8%
Confidence of increasing rate: 79.2%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.46° C
We are not 95% confident the trend is warming here and the median composite rose less than a half degree Celsius in 56 years, which is not a serious cause for alarm.
This is the last region to look at in our Four Weeks of Climate Data, so now we will go into recap mode, looking at what regions are showing serious increases of more than a degree C from 1955-2010 and which ones are not warming as fast, starting with our six slices of the Arctic.
Four weeks of climate data:
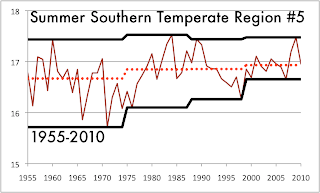
Southern Temperate Region #5
The fifth region of the Southern Temperate Zone is the last major land mass to be covered, as the last region which will be discussed later today is just two small islands in the south Atlantic.
As we can see, the actual land mass of Chile, Uruguay and Argentina is very well represented, as are a few islands both east and west.
The high temperature records haven't moved much in the Summer months, but the coldest Summers are getting warmer noticeably and the median has risen slightly.
Again, the record warmest in Fall is bouncing around, but the coldest Fall since the early 1970s has jumped up about a degree while the median is almost unchanged.
Winter gives us an idea of what data should look like if there was no overall trend.
Spring on the other hand shows upward movement in the low temperature measurement and two upward steps and one downward in the median and high measurement systems.
Confidence of the region warming: 97.7%
Confidence of decreasing rate: 88.5%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.15° C
There are important people in the history of statistics who were not in love with confidence tests, W. Edwards Deming being the best known. This data goes a long way towards proving Dr. Deming's point. We are confident of a warming trend because of 24 upward steps and 12 downward, and not quite confident of a slowing rate of warming because of 9 increasing steps and 15 decreasing steps. More to the point, 0.15° C is really small for 56 years.
Later today, two little islands in the middle of the South Atlantic get their say, our last data points covering the globe.
As we can see, the actual land mass of Chile, Uruguay and Argentina is very well represented, as are a few islands both east and west.
The high temperature records haven't moved much in the Summer months, but the coldest Summers are getting warmer noticeably and the median has risen slightly.
Again, the record warmest in Fall is bouncing around, but the coldest Fall since the early 1970s has jumped up about a degree while the median is almost unchanged.
Winter gives us an idea of what data should look like if there was no overall trend.
Spring on the other hand shows upward movement in the low temperature measurement and two upward steps and one downward in the median and high measurement systems.
Confidence of the region warming: 97.7%
Confidence of decreasing rate: 88.5%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.15° C
There are important people in the history of statistics who were not in love with confidence tests, W. Edwards Deming being the best known. This data goes a long way towards proving Dr. Deming's point. We are confident of a warming trend because of 24 upward steps and 12 downward, and not quite confident of a slowing rate of warming because of 9 increasing steps and 15 decreasing steps. More to the point, 0.15° C is really small for 56 years.
Later today, two little islands in the middle of the South Atlantic get their say, our last data points covering the globe.
Sunday, March 17, 2013
Four weeks of climate data:
Southern Temperate Region #4
Now we look at the temperate part of the South Pacific Ocean between New Zealand and South America.
Most of the famous South Pacific Islands are in the tropics. The best known of these islands are Easter Island, rightmost at (-105° long, -30° lat) and Pitcairn, where the Bounty mutineers settled, the second rightmost.
The low temperatures for Summer bounce around a lot, but the median shows steady increase.
Fall numbers show an increase at nearly every step.
Again, the low temperatures are bouncing around but the median grows steadily.
The cold Spring late last decade keeps this graph from showing steady increase everywhere.
Confidence of the region warming: 99.%
Confidence of decreasing rate: 65.8%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.45° C
We get a similar story to many of our regions. Yes, it's warming. No, we can't say if the rate is increasing or decreasing with any confidence and the amount of warming is in the range of a half degree Celsius in 56 years.
Tomorrow, our last two regions, Temperate South America and the temperate south Atlantic.
Most of the famous South Pacific Islands are in the tropics. The best known of these islands are Easter Island, rightmost at (-105° long, -30° lat) and Pitcairn, where the Bounty mutineers settled, the second rightmost.
The low temperatures for Summer bounce around a lot, but the median shows steady increase.
Fall numbers show an increase at nearly every step.
Again, the low temperatures are bouncing around but the median grows steadily.
The cold Spring late last decade keeps this graph from showing steady increase everywhere.
Confidence of the region warming: 99.%
Confidence of decreasing rate: 65.8%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.45° C
We get a similar story to many of our regions. Yes, it's warming. No, we can't say if the rate is increasing or decreasing with any confidence and the amount of warming is in the range of a half degree Celsius in 56 years.
Tomorrow, our last two regions, Temperate South America and the temperate south Atlantic.
Four weeks of climate data:
Southern Temperate Region #3
And now we hit a big clump of land the the Southern Temperate Zone, Australia and New Zealand.
Unlike that one island in the south Indian Ocean, most of the land here is between the 25th and 45th parallels, which makes for more moderate weather in general.
All three of our measurement systems have two upward steps and one downward step. The increase in the median from the first era to the last is less than half a degree.
In the Fall, the general trend of increase is more noticeable, but the difference in medians from first to last is slightly less that the Summer change.
The increasing trend is more noticeable in the Winters and the median jump is over a half degree.
Spring is bouncing up and down more randomly than the other seasons, but the median shows a steady increase of about a half a degree.
Confidence of the region warming: 99.9%
Confidence of decreasing rate: 65.8%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.44° C
We get a similar story to many of our regions. Yes, it's warming. No, we can't say if the rate is increasing or decreasing with any confidence and the amount of warming is in the range of a half degree Celsius in 56 years.
Later today, the fourth region, the Pacific islands between New Zealand and South America.
Unlike that one island in the south Indian Ocean, most of the land here is between the 25th and 45th parallels, which makes for more moderate weather in general.
All three of our measurement systems have two upward steps and one downward step. The increase in the median from the first era to the last is less than half a degree.
In the Fall, the general trend of increase is more noticeable, but the difference in medians from first to last is slightly less that the Summer change.
The increasing trend is more noticeable in the Winters and the median jump is over a half degree.
Spring is bouncing up and down more randomly than the other seasons, but the median shows a steady increase of about a half a degree.
Confidence of the region warming: 99.9%
Confidence of decreasing rate: 65.8%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.44° C
We get a similar story to many of our regions. Yes, it's warming. No, we can't say if the rate is increasing or decreasing with any confidence and the amount of warming is in the range of a half degree Celsius in 56 years.
Later today, the fourth region, the Pacific islands between New Zealand and South America.
Saturday, March 16, 2013
Four weeks of climate data:
Southern Temperate Region #2
The second region of the Southern Temperate Zone is the Indian Ocean with a few scattered islands.
There were only readings from a few islands, and the only weather station that kept consistent readings from 1955 to 2010 was on the French controlled island Kerguelen.
As I said earlier, this "temperate zone" is cold. This is down in The Fifties and Summer average temperatures wander between 3° C to 7° C. For Americans, that's between 37.4° F and 44.6° F.
Cold. The coldest metric shows an increase, but the median and high show that the 90s were a little warmer than the first decade of this century.
The Fall numbers look similar to Summer, only more so, the 90s warmer that The Oughts.
Winter's pattern is different. Generally we see an increase across all metrics, but very little overall.
Spring is like Winter, but all the metrics show the big jump between the 1955-1975 era and the 1975-1988 period.
Confidence of the region warming: 99%
Confidence of decreasing rate: 97.9%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.55° C
One island in an expanse of ocean, but it counts as a region. It's warming but the rate is slowing down and the level of warming over 56 years is not particularly alarming.
Tomorrow, Australia and New Zealand lumped together in the third region then the gap between New Zealand and South America as Region #4.
There were only readings from a few islands, and the only weather station that kept consistent readings from 1955 to 2010 was on the French controlled island Kerguelen.
As I said earlier, this "temperate zone" is cold. This is down in The Fifties and Summer average temperatures wander between 3° C to 7° C. For Americans, that's between 37.4° F and 44.6° F.
Cold. The coldest metric shows an increase, but the median and high show that the 90s were a little warmer than the first decade of this century.
The Fall numbers look similar to Summer, only more so, the 90s warmer that The Oughts.
Winter's pattern is different. Generally we see an increase across all metrics, but very little overall.
Spring is like Winter, but all the metrics show the big jump between the 1955-1975 era and the 1975-1988 period.
Confidence of the region warming: 99%
Confidence of decreasing rate: 97.9%
Change in median temperature from the 1955-1975 interval to the 1999-2010 interval: 0.55° C
One island in an expanse of ocean, but it counts as a region. It's warming but the rate is slowing down and the level of warming over 56 years is not particularly alarming.
Tomorrow, Australia and New Zealand lumped together in the third region then the gap between New Zealand and South America as Region #4.
Subscribe to:
Posts (Atom)