Triangle classification and circumcenters

On Monday, we started the discussion of the "center" of a triangle, put in quotation marks because it is too vague. The centroid is the center of gravity and is always in the interior of the triangle, but the circumcenter, the center of the circle that passes through all three vertices, does not have to be in the interior. Here are the three possibilities.

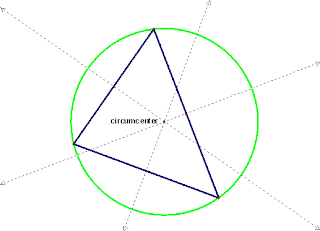
We are going to classify triangles by the size of the largest angle.  Since the angles always add up to 180°, we can only have one angle that is 90° or greater, and it is possible to have all the angles less than 90°.  If they are all less than 90°, the triangle is classified as acute and the circumcenter will be in the interior of the triangle.

The next possibility is that the largest angle is exactly 90°, which we call a right angle, so we classify these triangles as right triangles.  With a right traingle. the circumcenter will always be at the midpoint of the longest side, usually called the hypotenuse.

The last possibility is called an obtuse triangle, one whose largest angle is more than 90°. In this case, the circumcenter will not be in the triangle's interior.

Notice that a triangle inscribed in a circle creates three arcs. The total measure of those arcs is 360°. It turns out the measure of each arc is twice the measure of the angle that creates the arc. For example, if an inscribed triangle had angles 45°, 35° and 100°, the three arcs would measure 90°, 70° and 200° respectively. The center of the circle would inside the arc of 200° but outside the interior of the triangle itself.

(Note: all these illustrations were nicked from a webpage created by Kristina Dunbar of UGA.)

Tomorrow: the incenter of the triangle.